Objetivo de Aprendizaje

·         Identificar y definir los números, naturales, completos, enteros, racionales, irracionales y reales.

Introducción

Los matemáticos reconocen varios conjuntos de números que comparten ciertas características. Estas categorías son útiles cuando ciertos tipos de números son válidos para valores y variables. Nuestro entendimiento y clasificación de los diferentes conjuntos de números se ha desarrollado durante miles de años

                         

De Números Naturales a Enteros

Las primeras civilizaciones encontraron formas diferentes para escribir números, pero todas empezaron con el mismo conjunto de números que los niños de primaria aprenden hoy; los números naturales (también llamados números de conteo). Estos son los números 1, 2, 3, etc. — los números que usamos cuando contamos. Son naturales porque nuestro entendimiento de los números empieza con el reconocimiento de múltiples copias de cosas, como cuántos dedos tenemos, o el tamaño de conjuntos, como cuántos juguetes tenemos.

Aunque las civilizaciones más antiguas entendían "nada" — sabían cuando no tenían ninguna vaca, ni hijos, por supuesto — el número cero tiene una historia interesante. El primer uso de un símbolo para representar "nada" no fue sino hasta el siglo 3 AC. El sistema numérico Babilonio usaba los símbolos sólo como un marcador de posición en un sistema basado en posiciones, similar a la forma en que hoy usamos el 0 en el número 702 para representar no decenas. El primer reconocimiento del 0 como número, en la misma forma que 1 y 23 son números es incierto, pero puede datarse en el siglo 9 en India. Cuando se suma el 0 al conjunto de 1, 2, 3, etc., para formar los números completos. Estos se llaman "completos" porque no contienen fracciones.

Los enteros son números completos más sus contrapartes negativas: …, -3, -2, -1, 0, 1, 2, 3, …. Los números negativos aparecieron en China alrededor del siglo primero AC. (¡Eso es 1000 años antes que se reconociera al cero como número!) Sin embargo, a pesar de su utilidad para representar conceptos como deuda, no fue sino hasta el siglo 18 — hace menos de 300 años — que ganaron aceptación general como números.

   

Números Racionales

Los números fraccionarios han existido desde antes que los números negativos y el cero. Los Egipcios antiguos (a partir del siglo 21 AC) estudiaron las fracciones. Hoy en día, los números fraccionarios están incluidos en el conjunto de los números racionales, que son los números que se pueden escribir de la forma  donde p y q son enteros. Los números racionales pueden escribirse de muchas formas. Por ejemplo,  también puede escribirse como , 5.66…, o . Sin importar la forma en que sea usado, ya que este número puede ser escrito como el radio de dos enteros, el número es racional.

Hasta ahora, los tipos de números que hemos descrito forman una serie de conjuntos anidados. Empezamos con los números naturales, luego expandimos ese conjunto con el 0 para formar los números completos. Luego incluimos los números negativos con los números completos para crear los enteros. Ahora tenemos los números racionales, los cuales incluyen a todos los enteros además de muchos otros números.

Números Irracionales

El matemático Griego Pitágoras, de quien toma el nombre el Teorema de Pitágoras, era el líder de un grupo conocido como los Pitagóricos. Ellos creían que todas las cantidades podían ser expresadas con un número natural o una relación entre los números naturales. Cuenta la leyenda que creían esto tan fervientemente que cuando uno de sus miembros usó el Teorema de Pitágoras para demostrar que la hipotenusa del siguiente triángulo no puede ser expresada como el radio de números naturales, lo exiliaron.

Ahora sabemos que los Pitagóricos estaban equivocados, y que sí hay cantidades que no son racionales. Estos números irracionales no pueden ser expresados como el radio de enteros. Cualquier raíz cuadrada de un número que no sea un cuadrado perfecto, por ejemplo , es irracional.

Los números con una parte decimal pueden terminar o no terminar. Terminar significa que los dígitos eventualmente se detienen (aunque podemos escribir ceros al final). Un decimal que no termina tiene dígitos (diferentes de 0) que continúan para siempre. Por ejemplo, considera la forma decimal de , que es 0.3333…. Los 3s continúan indefinidamente. O la forma decimal de    , que es 0.090909…: la secuencia "09" continúa para siempre.

Además de no terminar, estos dos números son también decimales repetidos. Sus partes decimales están hechas de un número o secuencia de números que se repiten una y otra vez. Un decimal es no repetido si sus dígitos jamás forman un patrón repetitivo. El valor de , por ejemplo, es 1.414213562…. No importa qué tan lejos sigamos los números, los dígitos jamás repetirán la secuencia previa.

Si un número termina o se repite, debe ser racional; si no termina y no se repite, el número es irracional.

Considera un decimal que termina (o decimal terminal), como el 3.529. Como el número tiene un decimal que termina, no es un número racional. Podemos escribir 3.529 como el radio de dos enteros: el numerador es el número sin el punto decimal (en este caso 3,529) y el denominador es una potencia de 10 correspondiente al valor del lugar del último dígito. Como el 9 está en el lugar de las unidades de millar, el denominador es 1,000. (Otra forma de hacer esto es contar los lugares del punto decimal hacia la derecha del punto decimal en el número original. El denominador es 1 seguido de esa cantidad de 0s. Hay tres dígitos a la derecha del punto decimal en 3.529, por lo que el denominador es 1 seguido de tres 0s.) 

Números Reales

El conjunto de los números reales se forma al combinar el conjunto de números racionales y el conjunto de números irracionales. El conjunto de números reales consiste en todos los números que tienen un lugar en la recta numérica.     

Conjuntos de números Números naturales                   1, 2, 3, … Números completos                 0, 1, 2, 3, … Enteros                                    …, -3, -2, -1, 0, 1, 2, 3, … Números racionales                cualquier número que pueda ser expresado de la forma , donde p y q son enteros, los números racionales terminan o se repiten cuando son escritos en forma decimal Números irracionales              cualquier número que pueda ser expresado de la forma ,(donde p y q son enteros), los números irracionales no terminan y no se repiten cuando son escritos en forma decimal Números reales                       cualquier número que sea racional o irracional

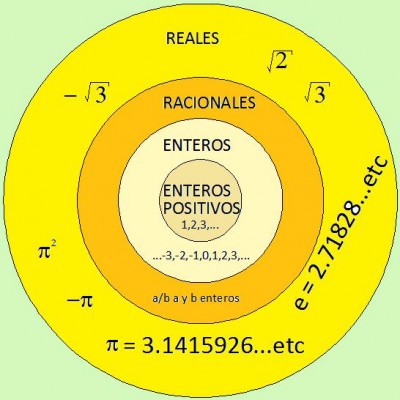
El diagrama siguiente muestra cómo todos los números reales se relacionan uno con otro. Nota que no hay superposición entre los números racionales y los números irracionales, y que ambos conjuntos forman los números reales.

Sumario

Los números que pueden ser representados en la recta numérica se llaman números reales. Estos números pueden ser separados en dos conjuntos que no tienen números en común: los números irracionales y los números racionales. Los números irracionales tienen formas decimales que no terminan ni se repiten. Los números racionales tienen formas decimales que terminan o se repiten. Dentro del conjunto de números racionales existen varios conjuntos más pequeños y que están anidados: los números enteros, números completos, y números naturales

Los conjuntos de números se definen como sigue:

Números reales	cualquier número que sea racional o irracional
Números racionales	cualquier número que se puede escribir como el radio de dos enteros y que termina o se repite en su forma decimal
Enteros	…, -3, -2, -1, 0, 1, 2, 3, …
Números completos	0, 1, 2, 3, …
Números naturales	1, 2, 3, …
Números irracionales	cualquier número que no se puede escribir como el radio de dos enteros y que no termina ni se repite en su forma decimal